Minimal Diamond-Saturated Families

Abstract

For a given fixed poset P we say that a family of subsets of [n] is P-saturated if it does not contain an induced copy of P, but whenever we add to it a new set, an induced copy of P is formed. The size of the smallest such family is denoted by sat^∗(n, P). For the diamond poset D₂ (the two-dimensional Boolean lattice), Martin, Smith and Walker proved that  ≤ sat^∗(n, D₂) ≤ n + 1. In this paper we prove that sat^∗(n, D₂) ≥ (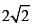−o(1)) 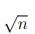. We also explore the properties that a diamond-saturated family of size c , for a constant c, would have to have.