Asymptotic Probability Expansions for Random Elements in a Hilbert space

Abstract

In this article, we approach a class of problems in probability theory, namely, the asymptotic expansion of probability. We consider an independent, identically distributed, and normalized stochastic process 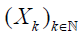in a separable Hilbert space H, and associate it with the normalized partial sum
.
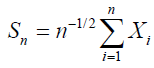As a result, we built on the ball with a fixed center asymptotic expansion of non-uniform probabilities; our conditions on the moments are minimal, and the dependency of estimates on the covariance operator is expressed with the terms of the eigenvalue series. Likewise, the covariance operators of the random elements do not coincide. In the open ball set with fixed center a and radius 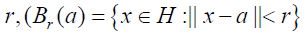, we estimate the optimal result of the Berry-Esseen type of the remainder, and the terms of the probability 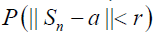by the Fourier method.