Dynamics of a SVEIR Epidemic Model with a Delay in Diagnosis in a Changing Environment

Abstract

A SVEIR epidemic model with a delay in diagnosis is studied in a constant and variable environment. The mathematical analysis shows that the dynamics of the model in the constant environment are completely determined by the magnitude of the delay-induced reproduction number 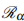. We established that if  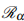< 1, the disease-free equilibrium is globally asymptotically stable, and when  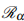> 1 the endemic equilibrium is globally asymptotically stable. In the variable environment, the model undergoes a transcritical bifurcation for 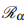= 1 leading to changes in the stability of the equilibrium points. The analytical effect of the delays in epidemic diagnosis is investigated. A minimum diagnosis rate α_min has been determined to face or control the disease effectively. Finally, numerical illustrations were presented to support the theoretical results.