Extreme Star of Phenylenes for the Merrifield-Simmons Index

Abstract

We identify extremal graphs concerning the number of independent sets for polyphenylene dendrimers. Specifically, we demonstrate that for a certain number of phenylenes, for example to k phenylenes, the compound formed as a star 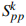 with a phenylene core achieves the maximum Merrifield-Simmons (M-S) index for a 1-connected component with an equal number of phenylenes. However, by relaxing the constraint of dendrimers to allow vertices with degrees greater than 3, it becomes possible to obtain topologies for compounds with a higher M-S index value. In this scenario, the starting point where every cut-edge is incident to the same vertex of the phenylene core emerges as the extremal topology concerning the M-S index for a 1-connected component with k phenylenes. These insights could facilitate the development of advanced molecular designs and contribute to enhanced performance in applications such as boiling points, drug delivery, molecular electronics and other nanotechnological innovations.