F-Hardy Rogers Type Contractions Endowed with Mann's Iterative Scheme in Convex Generalized b-Metric Spaces

Abstract

This article presents novel fixed point results using Mann’s iterative process in complete convex b-metric spaces, building upon Isa Yildirim’s recent work. The author established the definition of the 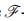-Hardy-Rogers contraction of the Nadler type by relaxing two conditions of Wardowski’s 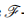-mapping. Our approach employs Mann’s iterative scheme in 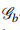-metric spaces under convex conditions. A supporting example with detailed calculations validates our result. Furthermore, we demonstrate the applicability of our findings by solving an integral equation through fixed point equation along with the axioms of the provided result. The obtained results are generalizations of several existing results in the literature.