Solvability of a Doubly Singular Boundary Value Problem Arising in Front Propagation for Reaction-Diffusion Equations
DOI:
https://doi.org/10.37256/cm.6120256084Keywords:
singular boudary value problems, reaction-diffusion-convection equations, travelling wave solutions, degenerate parabolic equations, speed of propagationAbstract
The paper deals with the solvability of the following doubly singular boundary value problem
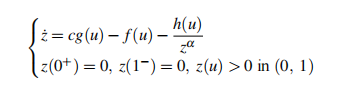
naturally arising in the study of the existence and properties of travelling waves for reaction-diffusion-convection equations
governed by the p-Laplacian operator. Here c, α are real parameters, with α > 0, and f, g, h are continuous functions in [0, 1], with
h(0) = h(1), h(u) > 0 in (0, 1).
Downloads
Published
2024-12-31
How to Cite
1.
Marcelli C. Solvability of a Doubly Singular Boundary Value Problem Arising in Front Propagation for Reaction-Diffusion Equations. Contemp. Math. [Internet]. 2024 Dec. 31 [cited 2025 Jan. 10];6(1):135-4. Available from: https://ojs.wiserpub.com/index.php/CM/article/view/6084
Issue
Section
Research Article
Categories
License
Copyright (c) 2024 Cristina Marcelli.
This work is licensed under a Creative Commons Attribution 4.0 International License.