On Solvability of Group Equations Over Torsion-Free Groups

Abstract

Let A be a group, ⟨t⟩ the free group generated by t, and let r(t) ∈ A∗ ⟨t⟩. The group equation r(t) = 1 is said to have a solution over A if a solution exists in some group containing A. In other words, this means that the canonical map A →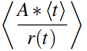  is injective. A group is said to be torsion-free if the order of every non-identity element is infinite. There is a conjecture (attributed to F. Levin) that every group equation over an arbitrary torsion-free group is solvable. It has been proved that this conjecture holds true for group equations of length at most seven. This study examines the solvability of group equations of length eight over a torsion-free group