Intrinsic Cheeger Energy for the Intrinsically Lipschitz Constants

Abstract

Recently, in metric spaces, Le Donne and the author have introduced the so-called intrinsically Lipschitz sections. The main aim of this note is to adapt Cheeger theory for the classical Lipschitz constants, in our new context. To be more precise, we define the intrinsic Cheeger energy from L²(Y, 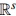) to [0, +∞],where (Y, d_Y , 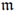) is a metric measure space and we characterize it in terms of a suitable notion of relaxed slope. In order to get this result, in a more general context, we have established some properties of the intrinsically Lipschitz constants like the Leibniz formula, the product formula and the upper semicontinuity of the asymptotic intrinsically Lipschitz constant.