Structure of Algebras Satisfying an ω-Polynomial Identity of Degree Six

Authors

Hamed Ouedraogo Department of Mathematics, Norbert Zongo University, Koudougou, Burkina Faso https://orcid.org/0009-0002-1505-3933
Daouda Kabré Department of Mathematics, Norbert Zongo University, Koudougou, Burkina Faso https://orcid.org/0009-0004-9862-2226
Abdoulaye Dembega Department of Mathematics, Norbert Zongo University, Koudougou, Burkina Faso
André Conseibo Department of Mathematics, Norbert Zongo University, Koudougou, Burkina Faso https://orcid.org/0000-0001-7424-273X

DOI:

https://doi.org/10.37256/cm.6220256453

Keywords:

idempotent, Peirce decomposition, ω-polynomial identity, Bernstein algebras, train algebras, evolution algebra

Abstract

This paper is devoted to the study of a class of commutative non-associative algebras characterized by the identity: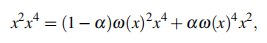

where α ∈ [0, 1]. In this study, we strongly use the Peirce decomposition technique. This allowed us to determine the conditions for an algebra of this class to be Bernstein, principal train, or evolution.

Downloads

Published

2025-03-19

How to Cite

Ouedraogo H, Daouda Kabré, Abdoulaye Dembega, André Conseibo. Structure of Algebras Satisfying an <i>ω</i>-Polynomial Identity of Degree Six. Contemp. Math. [Internet]. 2025 Mar. 19 [cited 2026 Feb. 8];6(2):1914-25. Available from: https://ojs.wiserpub.com/index.php/CM/article/view/6453

Download Citation

Issue

Contemporary Mathematics, Volume 6 Issue 2 (2025), 1380-2725

Section

Research Article

License

This work is licensed under a Creative Commons Attribution 4.0 International License.