Liouville Theorems and Gradient Estimates for Positive Solutions to Δpu + Δqu + h(u) = 0 on a Complete Manifold

Abstract

In this paper, we use the Saloff-Coste Sobolev inequality and Nash-Moser iteration method to study the local and global behaviors of positive solutions to the nonlinear elliptic equation ∆_pu+∆_qu+h_(u) = 0 defined on a complete Riemannian manifold (M, g) with Ricci lower bound, where q ≥ p > 1 are constants and 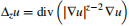 , with z ∈ {p, q}, is the usual z-Laplace operator. Under some assumptions on h(u), we derive gradient estimates and Liouville type theorems for positive solutions to the above equation. In particular, we show that, if an entire positive solution u to ∆_pu+∆_qu = 0 (1 < p ≤ q) on a complete non-compact Riemannian manifold M with non-negative Ricci curvature and dimM = n ≥ 3 satisfies

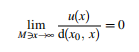
for some x₀∈ M, then u is a constant.