Well-Posedness of the Dispersion-Generalized Modified Benjamin-Ono Equation in Generalized Fourier-Lebesgue Spaces

Zijun Chen; Chunyan Huang

doi:10.37256/cm.6320256615

Well-Posedness of the Dispersion-Generalized Modified Benjamin-Ono Equation in Generalized Fourier-Lebesgue Spaces

Authors

Zijun Chen School of Mathematics and Statistics, Beijing Institute of Technology, Beijing, 100081, China https://orcid.org/0009-0000-4100-8058
Chunyan Huang School of Statistics and Mathematics, Central University of Finance and Economics, Beijing, 100081, China https://orcid.org/0000-0002-2535-6033

DOI:

https://doi.org/10.37256/cm.6320256615

Keywords:

dispersion-generalized modified Benjamin-Ono equations, local well-posedness, modulation spaces, Fourier-Lebesgue spaces

Abstract

We consider the Cauchy problem of the dispersion-generalized modified Benjamin-Ono equation on the real line with low-regularity initial data. To this motivation, we apply a generalized Fourier-Lebesgue space 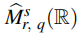, which serves as a unification of modulation spaces and Fourier-Lebesgue spaces. One of the key ingredients is an improved bilinear estimate and the well-posedness is obtained by perturbation arguments.

Downloads

Published

2025-06-09

How to Cite

Chen Z, Huang C. Well-Posedness of the Dispersion-Generalized Modified Benjamin-Ono Equation in Generalized Fourier-Lebesgue Spaces. Contemp. Math. [Internet]. 2025 Jun. 9 [cited 2026 Jun. 4];6(3):3537-61. Available from: https://ojs.wiserpub.com/index.php/CM/article/view/6615

Download Citation

Issue

Contemporary Mathematics, Volume 6 Issue 3 (2025), 2726-3845

Section

Research Article

License

This work is licensed under a Creative Commons Attribution 4.0 International License.