Construction of Quantum Codes from Constacyclic Codes Over the Class of Commutative Rings

Authors

Pushpendra Sharma Department of Mathematics, Faculty of Science, Aligarh Muslim University, Aligarh-202002, India https://orcid.org/0000-0002-5525-6658
Amal S. Alali Department of Mathematical Sciences, College of Science, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh- 11671, Saudi Arabia https://orcid.org/0000-0001-7856-2861
Shakir Ali Department of Mathematics, Faculty of Science, Aligarh Muslim University, Aligarh-202002, India https://orcid.org/0000-0001-5162-7522
Mohd Azeem Department of Mathematics, Faculty of Science, Aligarh Muslim University, Aligarh-202002, India https://orcid.org/0009-0001-5066-5946

DOI:

https://doi.org/10.37256/cm.6420257258

Keywords:

constacyclic code, Kronecker product, quantum code, Gray map, Linear Complementary Dual (LCD) code

Abstract

This paper primarily investigates the structural properties of constacyclic codes over the ring 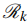, defined as 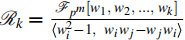where i, j = 1, 2, 3, ..., k, and k, m are positive integers. Here, 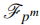denotes a finite field of order p^mwith characteristic p, an odd prime. Furthermore, we determine the necessary and sufficient conditions for the duals of constacyclic codes to exist. These findings make it easier to create new Quantum Error-Correcting (QEC) codes throughout the ring 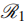(i.e., when k = 1), as well as optimal linear codes that make use of the Gray images of constacyclic codes. Additionally, Table 4 presents several Linear Complementary Dual (LCD) codes obtained using the Gray map.

Downloads

Published

2025-08-19

Issue

Contemporary Mathematics, Volume 6 Issue 4 (2025), 3846-5367

Section

Research Article

License

This work is licensed under a Creative Commons Attribution 4.0 International License.