Riemannian Manifolds Isometric to a Sphere

Abstract

To investigate the geometry of a Riemannian manifold(N^m, g), sometimes it is convenient to isometrically immerse it into the Euclidean space E^m+n, which is always possible through Nash's embedding Theorem provided that the codimension n is taken to be sufficiently high. The isometric immersion ψ : (N^m, g) → R^m+n can be treated as the position vector of points of N^m in R^m+n and therefore can be expressed as ψ = ξ + ψ^⊥, where ξ is tangential to N^m, whereas ψ^⊥ is normal to N^m. The Ricci tensor Ric of the Riemannian manifold (N^m, g) yields a symmetric operator Q, known as the Ricci operator, which satisfies the relation Ric (X, Y) = g(QX, Y). In this article, we consider the isometric immersion ψ : (N^m, g) → R^m+n of a compact Riemannian manifold (N^m, g) and show that if the tangential vector field ξ on (N^m, g) is an eigenvector of Q with constant eigenvalue 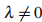, that is, Qξ = λξ , and the Ricci curvature Ric (ξ , ξ ) satisfies 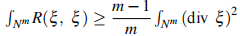, then (N^m, g) is necessarily isometric to the Euclidean sphere S^m(c) of constant curvature. Moreover, the converse also holds.