Existence of Scalar Minimizers for 0-Nonconvex Autonomous Single Integrals with Relaxed Lagrangian at Zero Velocity Having No Isolated Local Minimum Points

Abstract

We study the nonconvex integral 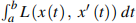, defined in the class of the absolutely continuous functions x : [a, b]  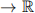having x(a) = A & x(b) = B, using a superlinear -measurable nonconvex lagrangian 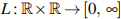 freely taking ∞ values and having L(s, ·) lower semicontinuous. Our aim is to look for weak hypotheses under which true minimizers still exist. In previous papers we have shown that 0-convexity L^∗∗ (·, 0) = L(·, 0) suffices provided L^∗∗ (·, ·) is lower semicontinuous at velocity zero, namely lsc at (s, 0) ∀s. In this paper we present sufficient conditions for existence of true minimizers in the 0-nonconvex case instead, i.e. L^∗∗ (·, 0) < L(·, 0). This is important because when a relaxed minimizer is not a true minimizer then there exists another relaxed minimizer y(·) which has a non-singleton constancy interval where y(·) ≡ s′ with L^∗∗ (s′ , 0) < L(s′ , 0). Our simplest hypothesis to avoid this is that sublevel sets of L^∗∗ (·, 0) contain no singletons, provided L^∗∗ (·, ·) and (L−L^∗∗)(·, ·) are both lsc at velocity zero. We also prove new necessary conditions.