Global Solvability of the Generalized Boussinesq System with Linear or Nonlinear Buoyancy Force

Abstract

This paper is devoted to the global solvability of the Boussinesq system with fractional Laplacian (−∆)^α in 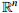 for n ≥ 3, where the buoyancy force has the form |θ|^m−1θe_n with m ≥ 1. By establishing estimates for the difference  |θ₁|^m−1θ₁ − |θ₂|^m−1θ₂ in Besov spaces and employing the maximal regularity property of (−∆)^α in Lorentz spaces, we prove the following results: under some reasonable assumptions on the exponents α, m, p, r and ρ, if the small initial data of velocity and temperature (or salinity) fall in  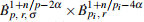(where p₁ = p for 1 < p < n, and p₂ = p/2 for n ≤ p < 2n) when m = 1, and in  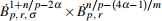when m > 1, then the generalized Boussinesq system admits a unique global strong solution (u, θ) in 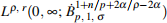×  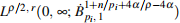(with i = 1, 2 cor-responding to the definition of p₁, p₂) for m = 1 and in 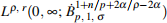×  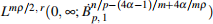for m > 1, respectively.