On Certain Normalized Classes Involving Higher-Order q-Derivatives

Abstract

The current research addresses the study of novel subclasses of analytic functions constructed within the open unit disk by employing a generalized operator based on q-calculus and higher-order q-derivatives. In particular, we introduce and investigate subclasses of multivalent analytic functions associated with the generalized operator 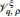. We establish several inclusion relations among these classes, highlighting the structural hierarchy induced by the parameterization of the q-operators. Additionally, we derive sharp coefficient inequalities of Fekete–Szegő type, providing precise bounds for the initial coefficients in the power series expansion of functions within these subclasses. The results presented extend and unify several existing findings in the theory of q-analytic functions and reduce to known results in the classical setting when the deformation parameter tends to one. The paper also presents sufficient conditions for class membership, discusses notable special cases, and offers new subordination results that connect these classes to stablished families of univalent functions. These contributions emphasize the importance of the generalized higher-order q-differential operator as a versatile tool in geometric function theory and underline the role of q-calculus in generating and analyzing rich families of analytic functions with potential applications beyond the classical framework.