Quantifying Uncertainty in HIV/AIDS Transmission: A Stochastic SEITA Model with Sensitivity Analysis

Abstract

Human Immunodeficiency Virus/Acquired Immune Deficiency Syndrome (HIV/AIDS) remains a global health crisis characterized by significant inherent uncertainties in transmission and intervention effectiveness, which are poorly captured by deterministic models. This study aims to develop a stochastic Susceptible-Exposed-Infected-Treated-AIDS (SEITA) model to quantify the impact of environmental and demographic noise on HIV/AIDS dynamics. This paper presents a stochastic extension of the classical SEITA model for HIV/AIDS transmission, incorporating treatment and vertical transmission pathways. Environmental and demographic variability are modeled through Ito-type Stochastic Differential Equations (SDEs). A novel stochastic reproduction number, 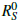, is derived, generalizing the deterministic threshold 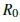. We rigorously establish that the infection dies out almost surely when  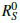< 1 (that is,  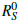≈ 0.87 in a representative scenario), and persists with positive probability when 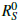> 1 (that, 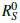≈ 2.08). Lyapunov-based stability analysis is conducted without relying on the deterministic endemic equilibrium. Numerical simulations, implemented via the Milstein method, demonstrate how stochastic fluctuations significantly affect long-term behavior; for instance, high noise intensities (σ = 0.2) can cause infected population fluctuations exceeding deterministic levels. These findings highlight the critical importance of incorporating stochasticity into epidemic modeling to improve prediction accuracy and inform robust public health strategies, particularly in resource-constrained settings where noise is inherent.