Transformation Semigroups Which Are Disjoint Union of Symmetric Groups

Abstract

Let T(X) be the full transformation semigroup on a set X. For an equivalence relation E on X, define a subsemigroup T_E∗(X) of T(X) by

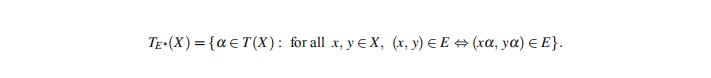
Let Q_E∗ (X) be the subset of T_E∗ (X) consisting of all transformations that each E-class contains exactly one element of its image. Then Q_E∗(X) forms a right group. In addition, for a nonempty subset Y of X, define S_Y (X) as a subset of T(X) consisting of all transformations mapping X onto Y such that the restriction on Y is a permutation. Then S_Y (X) is a left group. Furthermore, Q_E∗(X) and S_Y (X) can be expressed as a union of symmetric groups. This paper investigates some algebraic properties of Q_E∗ (X) and S_Y (X), calculates their ranks when X is finite, and establishes conditions for isomorphism. We also characterize and enumerate all maximal subsemigroups when X is finite. Finally, we address the problem of embedding arbitrary left groups into S_Y (X). Our results provide a complete algebraic classification of these transformation semigroups and demonstrate their significance as representations for right and left groups, thereby contributing to the broader understanding of transformation semigroups that decompose as unions of symmetric groups.