Fractal Analysis via Extended Fibonacci-Mann Iteration

Authors

Zaib Un Nisa Department of Mathematics, Quaid-i-Azam University, Islamabad-45320, Pakistan
Tayyab Kamran Department of Mathematics, Quaid-i-Azam University, Islamabad-45320, Pakistan
Umar Ishtiaq Office of Research, Innovation and Commercialization, University of Management and Technology, Lahore 54770, Pakistan https://orcid.org/0000-0002-5228-1073
Ioan-Lucian Popa Department of Computing, Mathematics, and Electronics, "1 Decembrie 1918" University of Alba Iulia, 510009 Alba Iulia
Mohammad Akram Department of Mathematics, Faculty of Science, Islamic University of Madinah, Madinah 42351, Saudi Arabia https://orcid.org/0000-0003-1416-5351

DOI:

https://doi.org/10.37256/cm.6620258103

Keywords:

Fixed point, convergence, iterative schemes, fractals

Abstract

In this paper, we propose an extended iteration of the generalized Fibonacci-Mann technique to establish an escape condition for functions of the form 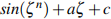，where a and c are complex constants, n ≥ 2, and is a complex variable. Using an s-convex combination framework, the proposed approach refines existing procedures and enables the generation of novel Mandelbrot and Julia sets. Furthermore, we provide numerical examples and graphic demonstrations to illustrate the efficiency of this novel technique.