On Spectrum of the Weakly Zero-Divisor Graph

Authors

Asif Imtiyaz Ahmad Khan Department of Mathematics, Aligarh Muslim University, Aligarh, 202002, India
Muzibur Rahman Mozumder Department of Mathematics, Aligarh Muslim University, Aligarh, 202002, India
Mohd Rashid Department of Mathematics, Aligarh Muslim University, Aligarh, 202002, India
Abu Zaid Ansari Department of Mathematics, Faculty of Science, Islamic University of Madinah, Madinah, K.S.A. https://orcid.org/0000-0001-6139-7521
Faiza Shujat Department of Mathematics, College of Science, Taibah University, Madinah, K.S.A.

DOI:

https://doi.org/10.37256/cm.6520258269

Keywords:

ring of integers modulo n, weakly zero-divisor graph, spectrum of graph, Seidel Laplacian and Seidel signless Laplacian spectrum

Abstract

Let us consider the finite commutative ring R, whose unity is 1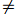0. The weakly zero-divisor graph, denoted by WΓ(R), is an undirected graph whose distinct vertices c₁ and c₂ are adjacent if and only if, there exist r ∈ ann(c₁) and s ∈ ann(c₂) that satisfy the condition rs = 0. This article finds the Seidel Laplacian and Seidel signless Laplacian spectrum for the graph WΓ(Z_n) for various values of n.

Downloads

Published

2025-09-24

Issue

Contemporary Mathematics, Volume 6 Issue 5 (2025)

Section

Research Article

License

This work is licensed under a Creative Commons Attribution 4.0 International License.