Stochastic SEIR Model with Two Infectious Classes Under Environmental Variability: Well-Posedness, Extinction Persistence Thresholds, and Milstein Based 3D Simulations

Abstract

We study a stochastic Susceptible-Exposed-Infectious-Recovered (SEIR) model with two infectious classes that capture behavioral heterogeneity: a primary (lower-compliance) class I_u and a secondary (higher-compliance) class I_u reached at rate σ. Transmission follows saturated incidence, and environmental variability is modeled by multiplicative mortality noise: a shared Brownian perturbation acting on S, E, R (intensitiesη_S, η_E, η_R) and an independent perturbation acting on I_v (intensity η_V ). We establish global existence, uniqueness, and positivity of solutions, and derive a noiseadjusted reproduction quantity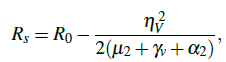 which provides a sufficient threshold: if R_s <1 the infection becomes extinct almost surely, whereas if R_s >1 the infection persists in the time-average sense. Milstein-based simulations using the same stochastic dynamics corroborate the analysis: subcritical regimes yield rapid fade-out, while supercritical regimes sustain transmission with substantial variability in peak size, timing, and time to extinction. Overall, randomness and compliance-driven heterogeneity materially reshape outbreak risk and should be accounted for when assessing control strategies near the threshold.