Geometric Vorticity and the Twofold Nature of Orthogonality

Abstract

Planar vector fields can be visualized using their tangent lines. It is shown that orthogonality between these curves and their associated orthogonal trajectories can be classified as well-ordered or irregular. Criterion for this taxonomy is the Global Curvature vector 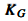 (a quantity involving the local curvatures of the two sets of lines) and in particular its rotation, 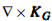. The latter, which has been termed Geometric Vorticity  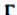is an important quantity for the characterization of a two-dimensional vector field. Depending on the kinematical constraints the field is subjected to, 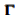can either vanish (well-ordered orthogonality) or not (irregular case). The main theorem of the study asserts that every Laplacian vector field is geometrically irrotational ( 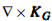= 0) and therefore well-ordered. Conversely, well-ordered orthogonal nets (which are sets of curves admitting zero geometric vorticity) can always be attributed to a Laplacian vector field. The necessary and sufficient condition for this behavior is the harmonicity of their angle function φ (∆φ = 0), which is defined as the angle of incidence of the field lines. This provides a pure geometric criterion a vector field should fulfill, in order to satisfy the Laplace conditions. It connects its “appearance” with its “nature”, thus allowing the experimentalist to study the violation of continuity and irrotationality in physical processes by mere observation.