Stable Truncated Trigonometric Moment Problems

Abstract

Let 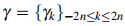,  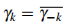be an one dimensional complex sequence of degree at most 2n. In the present paper we give a necessary condition such that  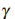admits on 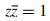an atomic representing measure with a finite number of atoms. The necessary condition is expressed in terms of "stability" of the Riesz linear non-negative functional, 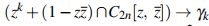, associated to the given sequence. We also give a necessary and sufficient condition such that the extended sequence  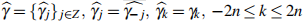to admit on 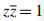an unique atomic representing measure with a finite number of atoms. The "stability" condition of the introduced Riesz functional is an adaption of the concept "dimension stability" by Vasilescu introduced for solving Hamburger moment problems in [5]. In section 3 of the present paper, we apply the main existence theorem for determining representing measures with 1, 2, 3 atoms, according to the rank of the moment matrix. The representing measures of the data of the quadratic moment problem have the support in the unit circle.