Geometric Features of a Multivalent Function Pertaining to Fractional Operators

Abstract

The Prabhakar fractional operator is commonly acclaimed as the queen model of fractional calculus. The distinction between univalent and multivalent functions became more formalized as part of the broader field of geometric function theory. This area of mathematics focuses on the study of analytic functions with specific geometric properties, such as injectivity, and their applications in various domains, including conformal mapping and potential theory. This paper’s goal is to discover new results of the harmonic multivalent functions 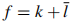 defined in the open unit disc 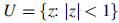. Let present 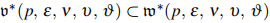, the class of multivalent harmonic functions of the form  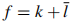in the open unit disc. Analyzing convolution with prabhahar fractional differential operator  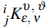with multivalent harmonic function to be in the class 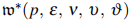. The coefficient inequality, growth rates, distortion properties, closure characteristics, neighborhood behaviors, and extreme points, all pertinent to this class  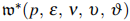were explored.