Dynamic Analysis of Extinction and Stationary Distribution of a Stochastic Dual-Strain SEIR Epidemic Model with Double Saturated Incidence Rates

Abstract

This study aims to enhance and extend the mathematical model of a dynamic stochastic dual-strain SEIR epidemic with a double-saturated incidence rate. The model is represented by a nonlinear system of differential equations that describe the dynamics of susceptible, exposed, infected and recovered individuals, with the exposed and infected compartments further divided into sub-classes for the first and second strains. We develop an innovative stochastic epidemic model where drug-sensitive and drug-resistant infected groups interact through mutation. The primary objective is to determine the existence and uniqueness of a positive global solution using a well-deservedly constructed Lyapunov function, enabling a deeper analysis of the system’s complexities. This analytical framework reveals the interactions between disease transmission, treatment dynamics, and stochastic influences. A significant contribution to this work is defining the stochastic basic reproduction number 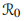as a threshold for the progression of both strains. Under low noise conditions and 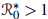, the model predicts the emergence of an ergodic stationary distribution, offering insights into longterm disease trends. Conversely, in high-noise scenarios, 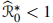, the analysis explores the extinction and persistence of drug-sensitive and drug-resistant infections. Our analytical results are further confirmed by simulations of epidemics spreading across drug-sensitive and drug-sensitive populations. Based on our simulations and theoretical predictions, we find that they are closely aligned.