Monte Carlo Approach Towards Evaluating Random Number Generators Based on Mathematical Schemes Driven from Chua's Circuit

Abstract

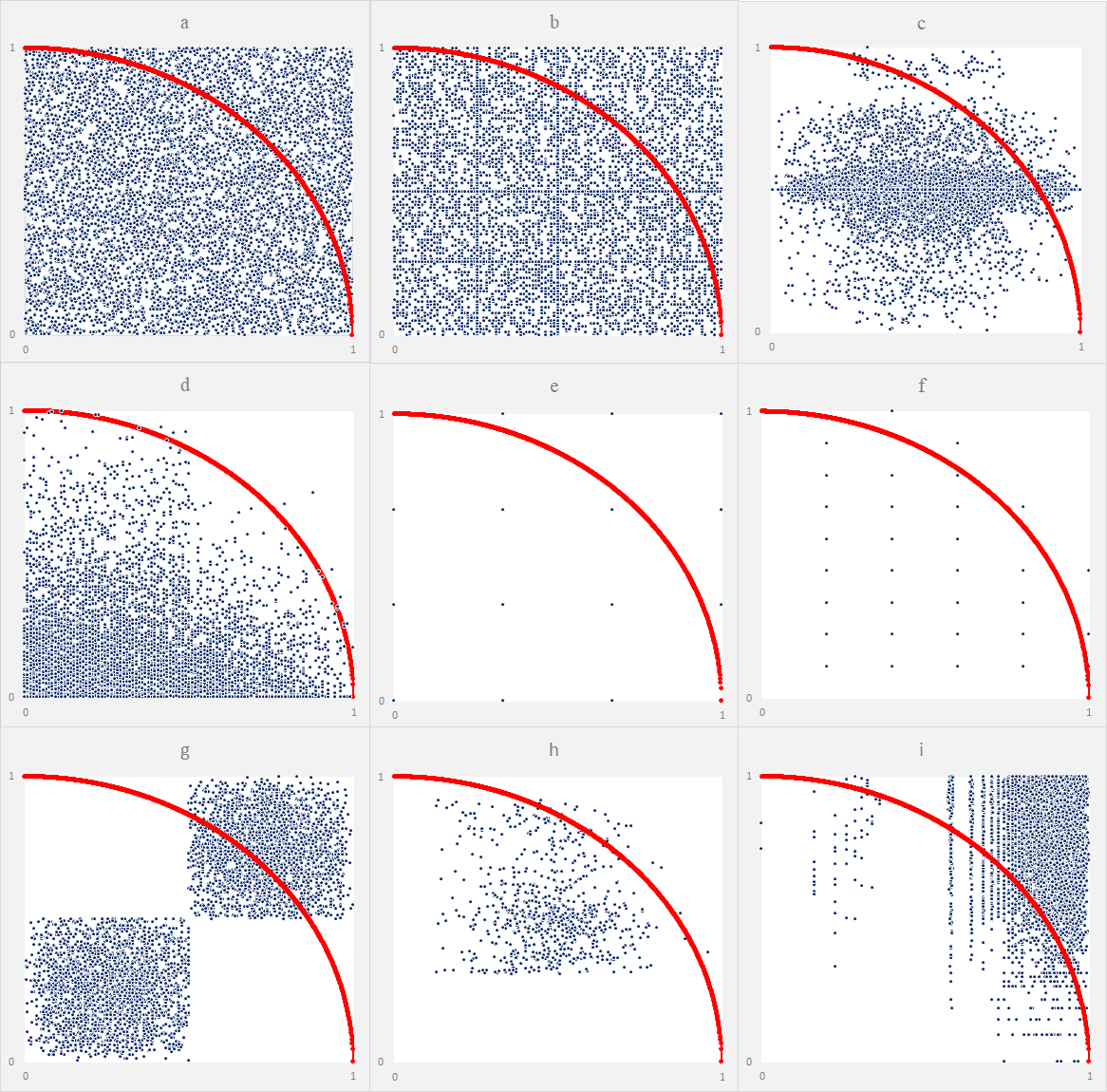
The philosophical nature of randomly generated quantities is widely discussed in the realms of chaos theory. Although, the fundamental premise of the chaos theory does not assume any random behavior in the resulting series and considers them deterministic, however highly dependent on the initial conditions of the system, one could address the problem of randomness, by using the output of a chaotic system, as the input of a mathematical function, aiming for the generation of randomly distributed values. For that matter, the voltages of the two capacitors in the classic configuration of a Chua's circuit have been measured. Having defined eight mathematical schemes for manipulating the inputted data set, the current manuscript focuses on the pragmatic and engineering criteria of the resulting data, in terms of randomness, and spectral distributions; hence proposing methods of random data generation. The ranking of schemes has been proceeded through a geometrical manifestation of the Monte Carlo Integration. And the suggested eight schemes are compared with the commercially common timer-based random generators. As the geometrical domain in the Monte Carlo Integration has defined in such a way that the most randomly distributed data set would result in a closer estimation of the number Pi, the suggested scheme working based on 'frequency indicator' is evaluated as the highest-ranked scheme in that regard, with  the estimated numerical value of 3.1424 for Pi.