Theta Pairing of Hypersurface Rings

Abstract

In this article, we prove a conjecture on the positive definiteness of the Hochster Theta pairing over a general isolated hypersurface singularity, namely: Let R be an admissible isolated hypersurface singularity of dimension n. If n is odd, then 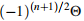 is positive semi-definite on 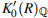. The conjecture is expected to be true for the polynomial ring over any field. We prove this conjecture over any field of arbitrary characteristic. We also provide two different proofs of the above conjecture overusing the Hodge theory of isolated hypersurface singularities and structural facts about the category of matrix factorizations. The first proof overis a more complete and developed version of a former work of the author. We have extended some of the former results in this article. The second proof overis quite direct and uses a former result of the author on Riemann-Hodge bilinear relations for Grothendieck residue pairing of isolated hypersurface singularities.