Deriving Optimal Skew Polycyclic Codes Over Fq Using Skew Polycyclic Linear Codes Over R = R1 ×R2 ×R3

Abstract

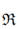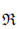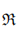This paper investigates the theory and applications of linear and skew polycyclic codes over the ring = 1 ×2 ×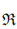3, where 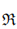i (0 ≤ i ≤ 3) are finite commutative rings. We first explore the structure of linear codes over 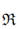, establishing foundational properties. Then, we introduce skew polycyclic codes over 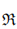, a generalization of polycyclic code over a finite field. We delve into the algebraic structure of these codes and demonstrate how they differ from their classical counterparts. Furthermore, we examine the dual codes ofskew polycyclic codes over 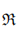, providing necessary and sufficient conditions for a code to be self-dual. Finally, we investigate the Gray images of skew polycyclic codes over 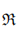, focusing on codes with optimal parameters. We provide explicit construction of Gray maps that yield images with good properties,such aslarge minimum distances and favorable automorphism groups. These results have potential applications in constructing new classes of error-correcting codes. We demonstrate this through an example of skew polycyclic codes applied in secret sharing schemes.