Using Skew Cyclic Codes Over R = R1×R2×R3 to Detect Skew Cyclic Codes Over Fq

Ouarda  Haddouche; Karima Chatouh

doi:10.37256/cm.5420245789

Using Skew Cyclic Codes Over R = R₁×R₂×R₃ to Detect Skew Cyclic Codes Over F_q

Authors

Ouarda Haddouche LAMIE Laboratory, Faculty of Economic, Commercial, and Management Sciences, Batna 1 University, Batna, Algeria https://orcid.org/0009-0003-8022-9429
Karima Chatouh LAMIE Laboratory, Faculty of Economic, Commercial, and Management Sciences, Batna 1 University, Batna, Algeria https://orcid.org/0000-0003-4061-1239

DOI:

https://doi.org/10.37256/cm.5420245789

Keywords:

linear codes, skew cyclic codes, gray map, optimal codes, automorphism

Abstract

This article investigates linear codes over the ring 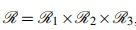, focusing on the properties and structure of skew cyclic codes within this framework. We explore various algebraic features of these codes, highlighting their distinctivenessfrom traditional cyclic codes. In addition, we examine the utility ofskew cyclic codes over 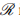in the context of identifying skew cyclic codes over the finite field 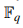with optimal parameters. The findings offer fresh perspectives on developing efficient and high-performing coding systems, which could benefit error correction and data transmission applications.

Downloads

Published

2024-12-23

How to Cite

Haddouche O, Chatouh K. Using Skew Cyclic Codes Over R = R1×R2×R3 to Detect Skew Cyclic Codes Over Fq. Contemp. Math. [Internet]. 2024 Dec. 23 [cited 2025 Jan. 21];5(4):6262-87. Available from: https://ojs.wiserpub.com/index.php/CM/article/view/5789

Download Citation

Issue

Contemporary Mathematics, Volume 5 Issue 4 (2024)

Section

Research Article

License

This work is licensed under a Creative Commons Attribution 4.0 International License.